import os, sys
from warnings import warn
import datetime as dt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import multivariate_normal
from gmm import MyGMM, ApproxGMM
from utils import make_blobs_gmm, plot_gaussians_2d, misclf_rate
from sklearn.mixture import GaussianMixture
%matplotlib inline
%reload_ext autoreload
%autoreload 2
from IPython.core.interactiveshell import InteractiveShell
from IPython.core.display import display, HTML
InteractiveShell.ast_node_interactivity = 'all' # display all output cells
display(HTML("<style>.container { width:100% !important; }</style>")) # make full width
pd.set_option('float_format', lambda x: '%.3f' % x)
pd.set_option('display.max_rows', 200)
np.set_printoptions(suppress=True)
Example in 1D
Generate dataset
from sklearn.datasets import make_blobs
from scipy.stats import norm
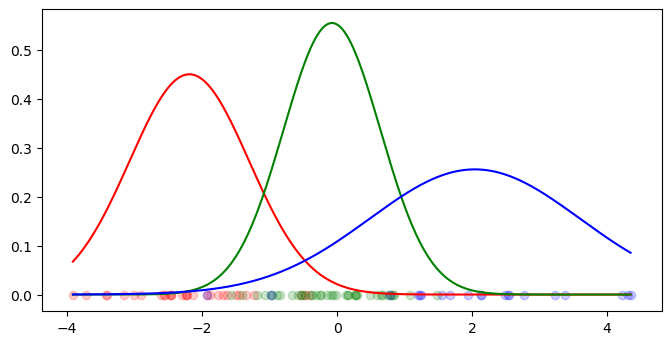
def make_dataset_1d(viz=True):
X, y = make_blobs(n_samples=[30, 40, 20],
n_features=1,
centers=[[-2], [0], [2]],
cluster_std=[1, 0.8, 1.5],
random_state=42)
X_by_class = np.asarray([X[y == c] for c in np.unique(y)])
mu_arr = np.asarray([X_cls.mean() for X_cls in X_by_class])
sigma_arr = np.asarray([X_cls.std() for X_cls in X_by_class])
if viz:
plt.subplots(figsize=(8, 4), dpi=100)
grid = np.linspace(X.min(), X.max(), 1000)
for i, c in enumerate('rgb'):
pdf = norm(mu_arr[i], sigma_arr[i]).pdf(grid)
plt.plot(grid, pdf, color=c)
plt.scatter(X_by_class[i], np.zeros_like(X_by_class[i]), color=c, alpha=0.2)
return X, y, mu_arr, sigma_arr
X, y, true_means, true_covariances = make_dataset_1d()
from dataclasses import dataclass
@dataclass
class Model():
means_: np.ndarray
covariances_: np.ndarray
truth = Model(true_means, true_covariances)
Our implementation
from typing import Tuple
class DIYGaussianMixture:
def __init__(self, c, random_state=None, verbose=False):
# Init params
self.c = c
self.x = None # data array
self.n = None # num rows
self.m = None # num dimensions
self.verbose = verbose
if random_state:
np.random.seed(random_state)
# Fitting params
self.is_fitted = False
self.means_ = None
self.covariances_ = None
def initialize_params(self, data: np.ndarray) -> Tuple[np.ndarray]:
""" initial random params before first iteration
Returns:
pi (c, 1): uniform prior on assignment to each cluster
mu: (c, m): location parameter of each cluster
cov (c, m, m): covariance matrices for each cluster
tau (n, c): weighted likelihood for each data point for each cluster
"""
self.x = data
self.n = data.shape[0]
self.m = data.shape[1]
# init π as uniform prior
pi = np.repeat(1 / self.c, self.c).reshape((-1, 1))
# init μ as random gaussian
# mu = KMeans(n_clusters=self.c).fit(data).cluster_centers_ # shape: (c, m)
mu = np.random.normal(size=(self.c, self.m))
# init Σ as identity matrix
cov = np.repeat([np.identity(self.m, dtype=np.float64)], self.c, axis=0)
return pi, mu, cov
def describe_arr(self, arr: np.ndarray, label: str) -> None:
""" Helper function to see shape of array between steps """
if self.verbose:
print('\n', f'{label}\tshape: {arr.shape}', '\n\n', arr, '\n')
def likelihood(self, mu, cov, x):
return multivariate_normal(mu, cov).pdf(x).astype(np.float64).flatten()
def e_step(self, pi, mu, cov):
""" Expectation step of EM algorithm """
self.describe_arr(mu, 'mu')
self.describe_arr(cov, 'cov')
# calculate likelihood vector of data points for each cluster k
tau = np.zeros(shape=(self.n, self.c))
# calculate likelihood vector of data points for each cluster k
for k in range(self.c):
tau[:, k] = self.likelihood(mu[k], cov[k], self.x)
log_lk = np.sum(np.log((tau * pi.flatten()).sum(axis=1)))
assert np.isinf(log_lk) == False, 'Log-likelihood must be finite'
if self.verbose: print(f'log_lk:\t{log_lk}')
# normalize likelihoods
tau /= tau.sum(axis=1).reshape(-1, 1)
# update π (assignment vector)
pi = tau.sum(axis=0) / self.n
self.describe_arr(pi, 'new pi')
return tau, pi, log_lk
def m_step(self, tau, pi):
""" Maximization step of EM algorithm """
mu = np.zeros(shape=(self.c, self.m))
cov = np.zeros(shape=(self.c, self.m, self.m))
for k in range(self.c):
# pull out reused calculations to simplify
cluster_weights = tau[:, [k]] # as shape (k, 1)
total_weights = cluster_weights.sum()
# update μ (mu vector)
mu[k, :] = (cluster_weights * self.x).sum(axis=0) / total_weights
# update Σ (covariance vector)
for i in range(self.n):
diff = (self.x[i] - mu[k]).reshape(-1, 1)
cov[k] += tau[i, k] * np.dot(diff, diff.T)
cov[k] /= total_weights
return mu, cov
def fit(self, data, iters: int = 100):
""" Fit EM algorithm to data """
pi, mu, cov = self.initialize_params(data)
scores = np.zeros(shape=iters)
for i in range(iters):
tau, pi, scores[i] = self.e_step(pi, mu, cov)
mu, cov = self.m_step(tau, pi)
self.scores_ = scores
self.means_ = mu
self.covariances_ = cov
self.pi = pi
self.is_fitted = True
return self
def predict_proba(self, data, pi, mu, cov):
assert self.is_fitted is True, 'Model must be fitted first'
tau, *_ = self.e_step(self.pi, mu, cov)
return tau
def predict(self, data):
mu, cov = self.means_, self.covariances_
probas = self.predict_proba(data, self.pi, mu, cov)
return probas.argmax(axis=1)
def fit_predict(self, data, iters=100):
self.fit(data, iters)
preds = self.predict(data)
return preds
gmm_1d = DIYGaussianMixture(c=3)
y_pred = gmm_1d.fit(X).predict(X)
Our model vs. reality
def gmm_accuracy(true_clusters, pred_clusters, true_means, pred_means):
""" Evaluate accuracy for n_clusters greater than 2 by relabeling clusters by predicted mean """
# Re-label true cluster membership by mean values (in ascending order)
y_sort_idx = true_means.flatten().argsort().argsort()
y_true_sorted = y_sort_idx[true_clusters]
# Re-label similarly for predicted cluster membership
y_pred_sort_idx = pred_means.flatten().argsort().argsort()
y_pred_sorted = y_pred_sort_idx[pred_clusters]
accuracy = (y_true_sorted == y_pred_sorted).mean()
return accuracy
def compare_gmm_models(true_model, fitted_model):
""" Plot conditional distributions for true and fitted models """
plt.subplots(figsize=(8, 4), dpi=100)
grid = np.linspace(X.min(), X.max(), 1000)
# plot for true model
true_model_sort_idx = true_model.means_.flatten().argsort()
sorted_true_means = true_model.means_.flatten()[true_model_sort_idx]
sorted_true_covariances = true_model.covariances_.flatten()[true_model_sort_idx]
for μ, σ, c in zip(sorted_true_means, sorted_true_covariances, 'rgb'):
pdf = norm(μ, σ).pdf(grid)
plt.plot(grid, pdf, color=c, alpha=0.2)
# plot for fitted model
fitted_model_sort_idx = fitted_model.means_.flatten().argsort()
sorted_fitted_means = fitted_model.means_.flatten()[fitted_model_sort_idx]
sorted_fitted_covariances = fitted_model.covariances_.flatten()[fitted_model_sort_idx]
for μ, σ, c in zip(sorted_fitted_means, sorted_fitted_covariances, 'rgb'):
pdf = norm(μ, σ).pdf(grid)
plt.plot(grid, pdf, color=c)
plt.show()
# Show a summary table comparing cluster means (true vs. predicted)
summary_df = pd.DataFrame([sorted_true_means, sorted_fitted_means], index=['True', 'Predicted'])
summary_df.columns.name = 'Cluster'
display(summary_df)
compare_gmm_models(truth, gmm_1d)
acc = gmm_accuracy(y, y_pred, true_means, gmm_1d.means_)
print(f'Accuracy: {acc:.2%}')
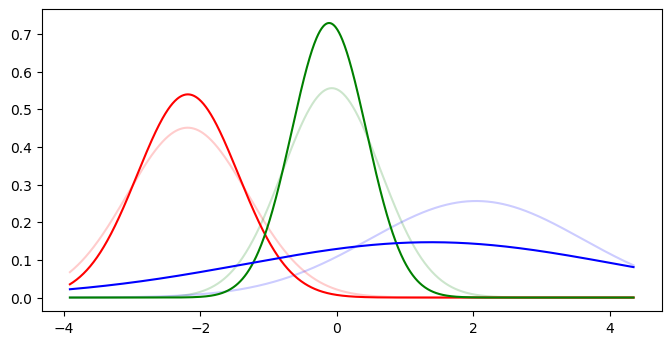
| Cluster | 0 | 1 | 2 |
|---|---|---|---|
| True | -2.188 | -0.076 | 2.040 |
| Predicted | -2.185 | -0.115 | 1.378 |
Scikit-learn vs. reality
from sklearn.mixture import GaussianMixture
sk_1d = GaussianMixture(n_components=3).fit(X)
sk_preds = sk_1d.predict(X)
compare_gmm_models(truth, sk_1d)
acc = evaluate_gmm_model(y, sk_preds, true_means, sk_1d.means_)
print(f'Accuracy: {acc:.2%}')
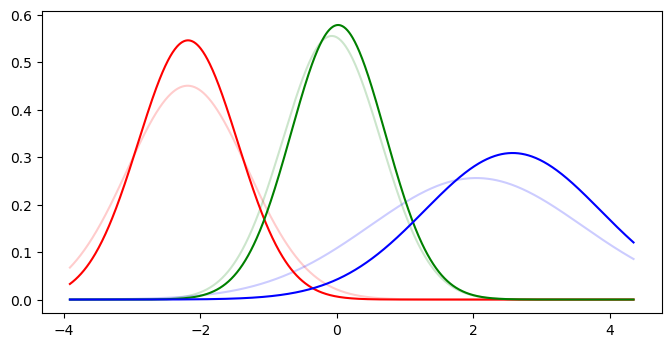
| Cluster | 0 | 1 | 2 |
|---|---|---|---|
| True | -2.188 | -0.076 | 2.040 |
| Predicted | -2.182 | 0.017 | 2.574 |
Accuracy: 87%
Our model vs. scikit-learn
agreement = gmm_accuracy(y_pred, sk_preds, gmm_1d.means_, sk_1d.means_)
print(f'Agreement: {agreement:.2%}')
Agreement: 92.22%
Example in 2D
Generate dataset
from sklearn.datasets import make_blobs
def make_blobs_gmm(n_features, viz=True, **kwargs):
""" Generate an ellipsoidal dataset suitable for GMM models """
XY, truth = make_blobs(n_features=n_features, random_state=42, **kwargs)
XY = np.dot(XY, np.random.RandomState(0).randn(n_features, n_features))
if viz and n_features <= 2:
plt.scatter(*XY.T, c=truth)
plt.show()
return XY, truth
_ = make_blobs_gmm(1)
benchmark_gmm(n_samples=[300, 100], n_features=1)
Benchmark GMM in 2D
benchmark_gmm(n_samples=[300, 100], n_features=2)
Example in 3D
Generate dataset
# generate a toy dataset for 2D
data_2d, truth_2d = make_blobs_gmm(n_samples=[350, 250],
n_features=2,
centers=None,
cluster_std=1,
viz=False)
model = ApproxGMM(c=2, verbose=False).fit(data_2d, iters=10)
preds_2d = model.predict(data_2d)
plot_gaussians_2d(data_2d, model.mu, model.cov, truth=truth_2d)
model.plot_likelihood()
plt.show()
Our implementation
Benchmark against scikit-learn
High dimensional dataset (MNIST)
Implement the EM algorithm for fitting a Gaussian mixture model for the MNIST dataset. We reduce the dataset to be only two cases, of digits “2” and “6” only. Thus, you will fit GMM with C = 2. Use the data file data.mat or data.dat on Canvas. True label of the data are also provided in label.mat and label.dat
Load dataset
Our implementation
Approximate
Benchmark ApproxGMM in 3D
data_3d, truth_3d = make_blobs_gmm(n_samples=50, n_features=3, centers=2, viz=False)
sk_3d = GaussianMixture(n_components=2, max_iter=10).fit(data_3d)
sk_preds = sk_3d.predict(data_3d)
print(f'sklearn mis-clf rate: {misclf_rate(truth_3d, sk_preds):.0%}')
gmm_3d = ApproxGMM(c=2).fit(data_3d, iters=10)
preds_3d = gmm_3d.predict(data_3d)
print(f'DIY mis-clf rate: {misclf_rate(truth_3d, preds_3d):.0%}')
comments powered by Disqus