What are hurdle models?
Google explains best,
The hurdle model is a two-part model that specifies one process for zero counts and another process for positive counts. The idea is that positive counts occur once a threshold is crossed, or put another way, a hurdle is cleared.
— Getting started with hurdle models [University of Virginia Library]
What are hurdle models useful for?
Many statistical learning models—particularly linear models—assume some level of normality in the response variable being predicted. If we have a dataset with a heavily skewed response or one which contains extreme outliers, it is a common practice to apply something like a Box-Cox power transformation before fitting.
But what do you do if you come across a clearly multi-modal distribution like the one below? Applying a power transform here will just change the scale of the variable, it won’t help with the fact that there is a huge spike of values at zero. The fact that it is multi-modal is a good indicator that we are over-aggregating data which belong to two or more distinct underlying data generation processes.
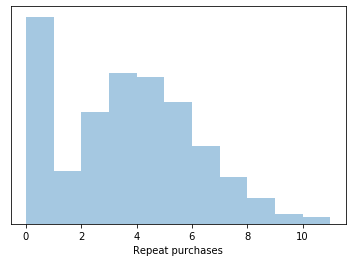
Distributions like this are commonly seen when analyzing composite variables such as insurance claims, where some large proportion are zero, but then the proportion of non-zero values take on a distribution of their own. Breaking down these sorts of distributions into their component parts allows us to more effetively model each piece and then recombine them at a later stage.
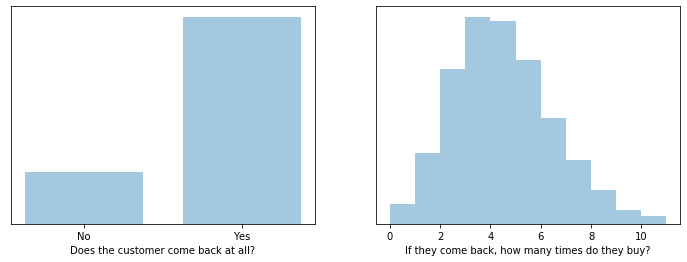
In the toy example above we have two underlying processes: Does a customer come back? If so, how many purchases does he or she make? The first is modeled as a binomial random variable (coin flip) and the second as a $ \text{Pois}(\lambda=4) $ random variable, which represents discrete event counts.
How can I implement a hurdle model?
So we want to fit and predict two sub-models, and then multiply their predictions together:
- A classifier, trained and tested on all of our data.
- A regressor, trained only on true positive samples, but used to make predictions on all test data.
The most straightforward way to achieve this would be to just train two separate models, make predictions on the same test dataset, and multiply their predictions together before evaluating. However with this approach we lose the ability to interface our model with the rest of the scikit-learn ecosystem, including passing it into GridSearchCV or any of the evaluation functions such as cross_val_predict.
A better approach is to implement our hurdle model as a valid scikit-learn estimator object by extending from the provided BaseEstimator class.
| from typing import Optional, Union | |
| import numpy as np | |
| import pandas as pd | |
| from sklearn.linear_model import LinearRegression, LogisticRegression | |
| from sklearn.base import BaseEstimator | |
| from sklearn.utils.estimator_checks import check_estimator | |
| from sklearn.utils.validation import check_X_y, check_array, check_is_fitted | |
| from lightgbm import LGBMClassifier, LGBMRegressor | |
| class HurdleRegression(BaseEstimator): | |
| """ Regression model which handles excessive zeros by fitting a two-part model and combining predictions: | |
| 1) binary classifier | |
| 2) continuous regression | |
| Implementeted as a valid sklearn estimator, so it can be used in pipelines and GridSearch objects. | |
| Args: | |
| clf_name: currently supports either 'logistic' or 'LGBMClassifier' | |
| reg_name: currently supports either 'linear' or 'LGBMRegressor' | |
| clf_params: dict of parameters to pass to classifier sub-model when initialized | |
| reg_params: dict of parameters to pass to regression sub-model when initialized | |
| """ | |
| def __init__(self, | |
| clf_name: str = 'logistic', | |
| reg_name: str = 'linear', | |
| clf_params: Optional[dict] = None, | |
| reg_params: Optional[dict] = None): | |
| self.clf_name = clf_name | |
| self.reg_name = reg_name | |
| self.clf_params = clf_params | |
| self.reg_params = reg_params | |
| @staticmethod | |
| def _resolve_estimator(func_name: str): | |
| """ Lookup table for supported estimators. | |
| This is necessary because sklearn estimator default arguments | |
| must pass equality test, and instantiated sub-estimators are not equal. """ | |
| funcs = {'linear': LinearRegression(), | |
| 'logistic': LogisticRegression(solver='liblinear'), | |
| 'LGBMRegressor': LGBMRegressor(n_estimators=50), | |
| 'LGBMClassifier': LGBMClassifier(n_estimators=50)} | |
| return funcs[func_name] | |
| def fit(self, | |
| X: Union[np.ndarray, pd.DataFrame], | |
| y: Union[np.ndarray, pd.Series]): | |
| X, y = check_X_y(X, y, dtype=None, | |
| accept_sparse=False, | |
| accept_large_sparse=False, | |
| force_all_finite='allow-nan') | |
| if X.shape[1] < 2: | |
| raise ValueError('Cannot fit model when n_features = 1') | |
| self.clf_ = self._resolve_estimator(self.clf_name) | |
| if self.clf_params: | |
| self.clf_.set_params(**self.clf_params) | |
| self.clf_.fit(X, y > 0) | |
| self.reg_ = self._resolve_estimator(self.reg_name) | |
| if self.reg_params: | |
| self.reg_.set_params(**self.reg_params) | |
| self.reg_.fit(X[y > 0], y[y > 0]) | |
| self.is_fitted_ = True | |
| return self | |
| def predict(self, X: Union[np.ndarray, pd.DataFrame]): | |
| """ Predict combined response using binary classification outcome """ | |
| X = check_array(X, accept_sparse=False, accept_large_sparse=False) | |
| check_is_fitted(self, 'is_fitted_') | |
| return self.clf_.predict(X) * self.reg_.predict(X) | |
| def predict_expected_value(self, X: Union[np.ndarray, pd.DataFrame]): | |
| """ Predict combined response using probabilistic classification outcome """ | |
| X = check_array(X, accept_sparse=False, accept_large_sparse=False) | |
| check_is_fitted(self, 'is_fitted_') | |
| return self.clf_.predict_proba(X)[:, 1] * self.reg_.predict(X) | |
| def manual_test(): | |
| """ Validate estimator using sklearn's provided utility and ensure it can fit and predict on fake dataset. """ | |
| check_estimator(HurdleRegression) | |
| from sklearn.datasets import make_regression | |
| X, y = make_regression() | |
| reg = HurdleRegression() | |
| reg.fit(X, y) | |
| reg.predict(X) | |
| if __name__ == '__main__': | |
| manual_test() |
Making it a valid Scikit-Learn estimator
The code snippet above may feel like it is longer than it needs to be. This is primarily because I tried to write it as a valid scikit-learn estimator, which I learned involves jumping through a few hoops so that it is compatible with other sklearn functions, including:
- Init variables must each be of a data type which evaluates as equal when compared with another copy of itself. This is necessary because sklearn clones estimators behind the scenes to do parallel processing in functions such as
GridSearchCv. Primitive datatypes (e.g.'yo' == 'yo'and42 == 42) pass this test, but already-initialized estimators to use as sub-models do not. Because of this, I pass model type as a string, then use the_resolve_estimatormethod to instantiate the actual estimator. - The
fitmethod returns the estimator itself, to enable method chaining. - The attribute
self.is_fitted_is set by the.fit()method and then checked by.predict(). - Any input is validated using the
check_array()function before being fit or predicted.
Scikit-learn provides a check_estimator function which runs a battery of automated tests against your estimator. I learned most of these requirements above while attempting to pass these tests.
Further reading
Rolling your own estimator [scikit-learn docs] – Provides a good overview of how to write your own estimator
Github / NeverForged / Hurdle [Github] – I used this as a starting point for my code.
Creating your own estimator in scikit-learn – Some additional concerns w.r.t GridSearchCV