from typing import Optional, Union, Tuple
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
%reload_ext autoreload
%autoreload 2
from IPython.core.interactiveshell import InteractiveShell
from IPython.core.display import display, HTML
InteractiveShell.ast_node_interactivity = 'all' # display all output cells
display(HTML("<style>.container { width:100% !important; }</style>")) # make full width
pd.set_option('float_format', lambda x: '%.3f' % x)
pd.set_option('display.max_rows', 200)
np.set_printoptions(suppress=True, linewidth=180)
Helper functions
def plot_kmeans(data: np.ndarray, clusters: np.ndarray, assignments: Optional[np.ndarray]=None) -> None:
""" Visualize data points, cluster centroids, and cluster assignments at a particular iteration of k-means. """
fig, ax = plt.subplots(figsize=(5, 5), dpi=100)
# Format grid
ax.grid(zorder=1)
ax.axvline(0, c='black', zorder=2)
ax.axhline(0, c='black', zorder=2)
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
# Plot data points
if assignments is None:
color = 'grey'
else:
color = np.asarray(['indianred', 'cornflowerblue'])[assignments]
ax.scatter(*data.T, s=256, c=color, edgecolors='black', zorder=3)
# Plot clusters
ax.scatter(*clusters.T, s=256, c=['darkred', 'darkblue'], marker='s', edgecolors='black', zorder=3)
for i, (x, y) in enumerate(data):
ax.annotate(i+1, (x, y), c='white', size=10, ha='center', va='center')
Step by step
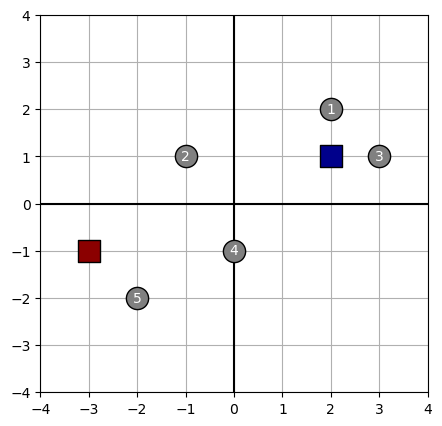
Let’s run k-means on a simple toy dataset and see what happens at each step.
data = np.asarray([
[2, 2],
[-1, 1],
[3, 1],
[0, -1],
[-2, -2]
])
centroids = np.asarray([
[-3, -1],
[2, 1]
])
plot_kmeans(data, centroids)
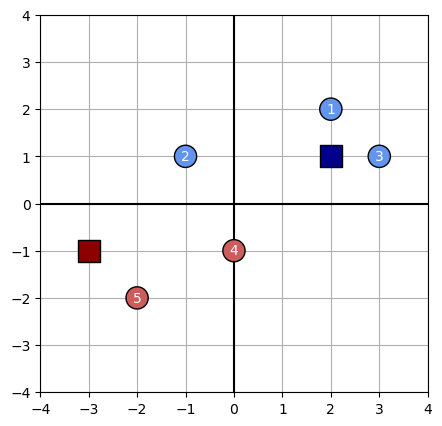
Show the cluster assignment
We assign each observation to the cluster whose centroid is closest: $\pi(i) = \text{argmin}_{j} \ | x_i - c_j |$ using the Manhattam $\ell_1$ norm. This results in data points 2, 4 and 5 being assigned to Cluster A, and data points 1 and 3 being assigned to cluster B.
def assign_data_points(data, centroids, norm=1):
distances = np.array([np.linalg.norm(data - centroid, ord=norm, axis=1) for centroid in centroids])
return np.argmin(distances, axis=0)
assignments = assign_data_points(data, centroids, norm=1)
plot_kmeans(data, centroids, assignments)
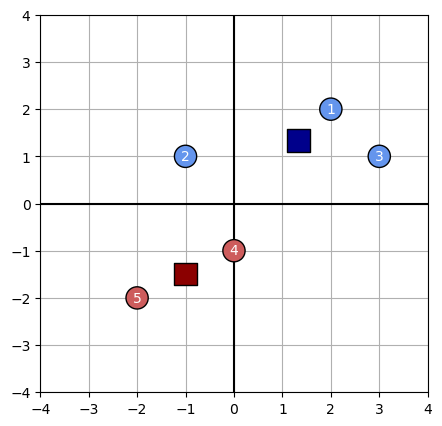
Show the location of the new center
We compute each cluster centroid as the average of each feature value for that cluster’s members: $c_j = \frac{1}{n_j} \sum_i^{n_j} x_i$
def adjust_centroids(data, assignments, k):
return np.array([np.mean(data[assignments == i], axis=0) for i in range(k)])
centroids = adjust_centroids(data, assignments, k=2)
plot_kmeans(data, centroids, assignments)
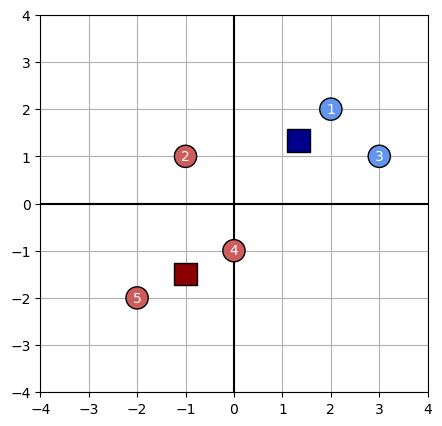
Will it terminate in one step?
The k-means algorithm terminates when the assignments made in an iteration do not change. In our case, the algorithm will not terminate, because in the next iteration data point #2 will be reassigned from Cluster B to cluster A. This occurs because we are using the $\ell_1$ norm, so the distance $d(x_2, A) = 2.5$ is smaller than $d(x_2, B) = 2.66$.
assignments = assign_data_points(data, centroids, norm=1)
plot_kmeans(data, centroids, assignments)
Rolling our own estimator
Base class
First we’ll define a base class which handles some of the boilerplate that is not specific to k-means: initializing clusters, looping, etc.
class Clustering(object):
def __init__(self, k: int):
""" Abtract base class for a clustering algorithm. """
self.data = None
self.k = k
self.centroids = None
self.assignments = None
def init_centroids(self, method: Union[str, np.ndarray]):
""" Initialize centroids according to a common method or by passing coordinates manually.
Args:
method: the two supported methods are 'forgy' and 'random_partition'
"""
n_rows = self.data.shape[0]
if isinstance(method, np.ndarray):
self.centroids = method
elif method == 'forgy':
self.centroids = self.data[np.random.randint(0, n_rows + 1, size=self.k)]
elif method == 'random_partition':
self.assignments = np.random.randint(0, self.k+1, size=n_rows)
self.centroids = self.adjust_centroids()
else:
raise NotImplementedError
def assign_data_points(self):
raise NotImplementedError
def adjust_centroids(self):
raise NotImplementedError
def fit_predict(self, data: np.array, init_method='forgy', max_iters=200, *args, **kwargs) -> Tuple[np.array, np.array]:
""" Iteratively assign data points to cluster and recompute cluster centers until converged.
Returns:
assignments: index of cluster to which each data point is assigned
centroids: final centroids after convergence
"""
# initialize centroids according to specified method
self.data = data
self.init_centroids(init_method)
# loop until centroids do not change
iter_idx = 0
while iter_idx < max_iters:
# assign each row to nearest cluster
self.assignments = self.assign_data_points()
# adjust cluster centers
new_centroids = self.adjust_centroids()
if (new_centroids == self.centroids).all():
break
else:
self.centroids = new_centroids
iter_idx += 1
print('.', end='')
if iter_idx == max_iters:
print('REACHED MAX ITERATIONS')
print('')
return self.assignments, self.centroids
K-means
To implement k-means, we can inherit from our base Clustering class and implement the logic for assigning data points and adjusting centroids.
class KMeans(Clustering):
def assign_data_points(self):
distances = np.array([np.linalg.norm(self.data - centroid, ord=1, axis=1) for centroid in self.centroids])
assignments = np.argmin(distances, axis=0)
return assignments
def adjust_centroids(self):
return np.array([np.mean(self.data[self.assignments == i], axis=0) for i in range(self.k)])
K-medoids
class KMedoids(Clustering):
def assign_data_points(self):
""" Assign data points to closest centroid, using either L1 or L2 norm """
if self.norm == 'L1':
ord = 1
else:
ord = None
distances = np.array([np.linalg.norm(self.data - centroid, ord=ord, axis=1) for centroid in self.centroids])
assignments = np.argmin(distances, axis=0)
return assignments
def adjust_centroids(self) -> np.ndarray:
""" Adjust centroids to be least dissimilar data point within, using either L1 or L2 norm """
if self.norm == 'L1':
metric = 'cityblock'
elif self.norm == 'L2':
metric = 'euclidean'
else:
raise NotImplementedError
centroids = np.zeros(shape=(self.k, self.data.shape[1]))
for j in range(self.k):
cluster_members = np.unique(self.data[self.assignments == j], axis=0)
avg_distances = np.mean(distance.cdist(cluster_members, cluster_members, metric=metric), axis=1)
centroids[j] = cluster_members[avg_distances.argmin()]
return centroids
comments powered by Disqus